Machine learning and advanced statistical analysis
Quantifying the similarity between planetary systems for unsupervised machine learning
Comparing results of single planet formation models with observations is relatively easy. For example, use the Euclidean distance in the space of features of planets (e.g. mass and period). In the case of planetary systems with more than one planet, this is more difficult, since a planetary system is formally a set of points in the feature space. In order to circumvent this difficulty, we have developed in this paper by Yann Alibert a new distance in the space of planetary system . The distance can be used in a variety of unsupervised machine learning algorithms, as for example visualisation techniques.
Dimensionality reduction and T-SNE visualization
We have use T-SNE in order to visualize results of planet formation models. An example is provided on the video below which shows the T-SNE minimisation, and where each point represents a planetary system with up to 10 planets. On this visualization, the distance between two points is related to the similarity between planetary systems. The similarity between systems is correlated with the number of planets in the system (a quantity that is not known by the visualization algorithm).
TSNE reflecting planetary system similarity
The similarity between planetary systems should be related to the similarity of the disks in which they form. To check this, run the video below! The location of points (each of them representing a planetary system) will evolve. It reflects at the beginning the similarity between systems, and at the end of the video the similarity between disks in which the systems were formed. The color of the points is kept unchanged during the video. At the end of the video, the similarity of colors reflects the similarity of disks, whereas the similarity of location reflects the similarity of disks. As can be seen, both are correlated, meaning similar protoplanetary disks give birth to similar planetary systems.
Using Deep Learning to compute planetary structure
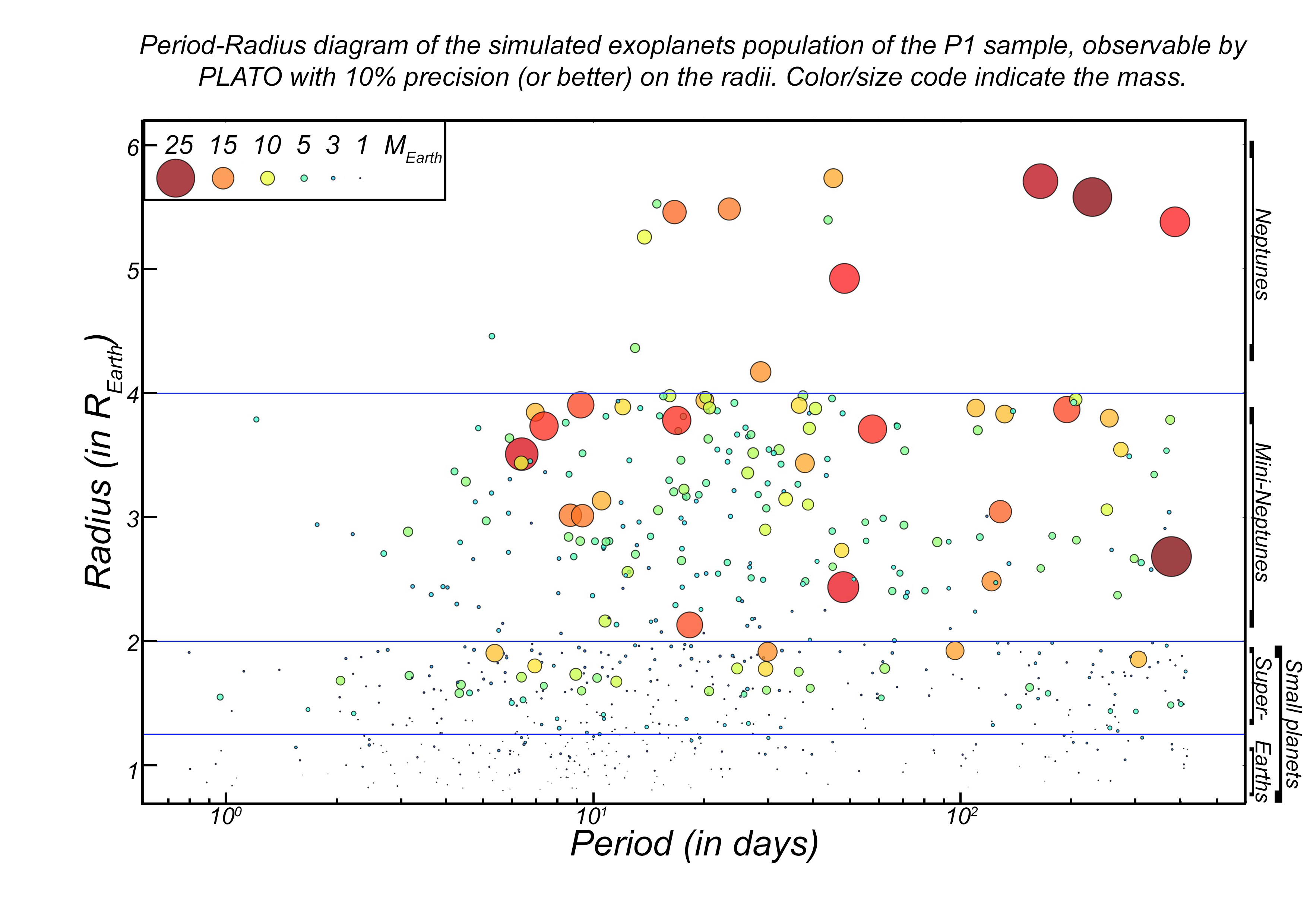
One key step of planet formation model is the computation of the mass of the planetary envelope. This mass depends on a variety of thermodynamical conditions, and must be computed by solving a set of differential equations. With Yann Alibert and Julia Venturini, we have trained a Deep Neural Network (DNN) in order to predict the mass of planetary envelopes, without having to solve these differential equations. By training the DNN on tens of millions of internal structure calculations, we have been able to reach a very good precision accuracy (of the order of percents). This is much better than the analytical relations one can find in the literature, and allows computing very rapidly planetary envelop mass with a very good accuracy. The codes to use our DNNs is available on GitHub, and the paper describing the method can be found here.
The figure below shows the comparison between the exact results (red), the results of the DNN (blue), and the results obtained using the analytical formulas from Ikoma et al. (2000) and Bitsch et al. (2015) for a planet forming in different conditions (see title of the graphs).
Advanced statistical tools: internal structure of low-mass planets
In preparation of CHEOPS data, we have, with Jonas Haldemann, developed advanced statistical methods to infer the internal composition of low-mass planets. For this, we have improved the MCMC scheme developed by Caroline Dorn (project 2.4 – see this recent paper and references therein) to speed up the calculations. Part of this effort is to develop a neural network to compute the internal structure of planets, in a way similar to what is presented above.
In the following animation we see samples of our new adaptive MCMC method given a planetary target of ~1 Earth mass, ~1 Earth radii and stellar composition in Fe/Si, Mg/Si. The three parameters (total Mass, total radius and Fe/Si mass fraction) represent a subset of the input and output parameters used in the calculation of the planetary structure model. The results of such an MCMC run are posterior probability distributions of those parameters. The few points in the upper region of the animation are points where the MCMC “walks” from its initialization point to the region of highest likelihood.
MCMC samples for a fiducial CHEOPS target
Invertible Neural Network for internal structure retrieval
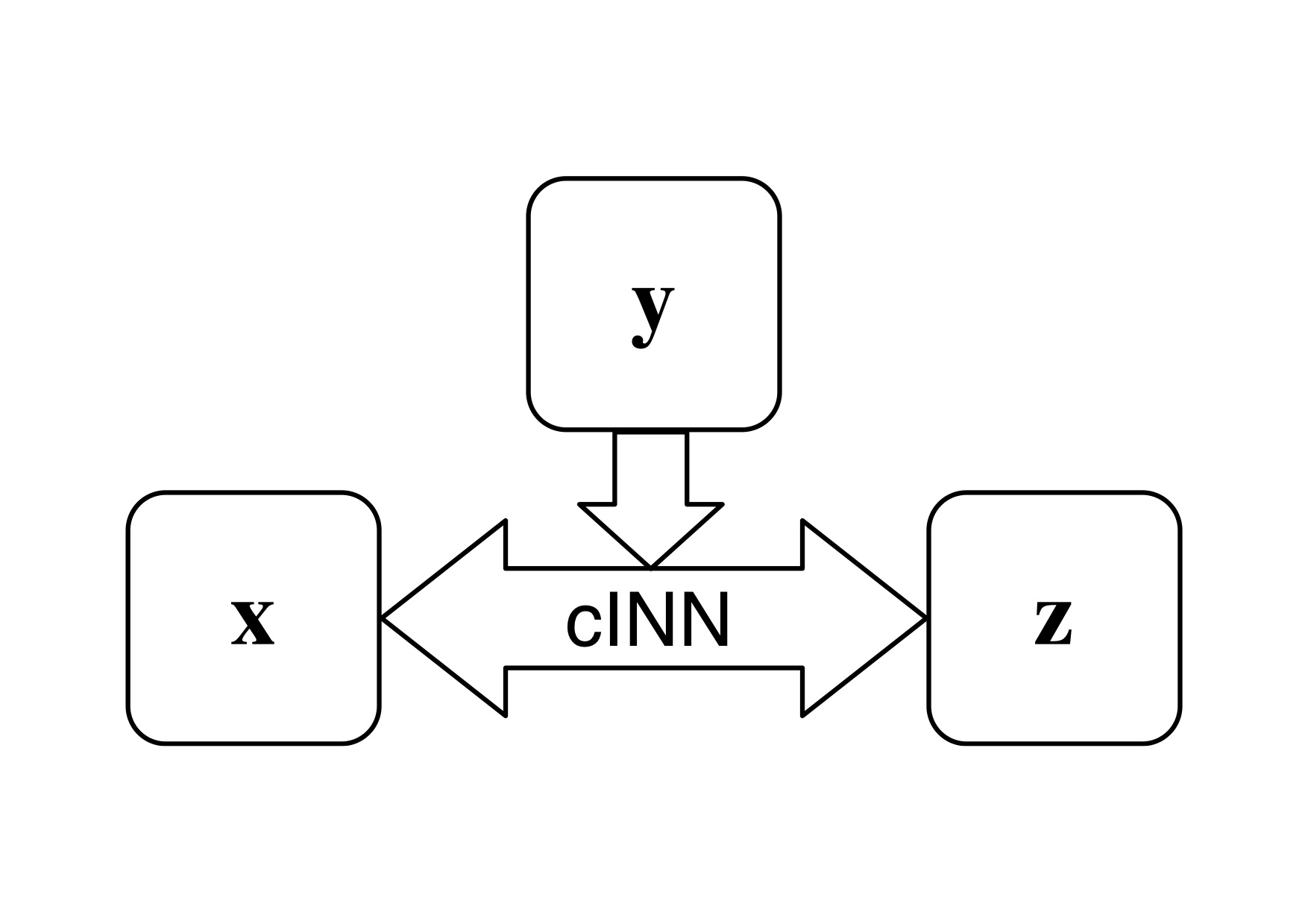
Constraining the internal structure of exoplanets from measurements of their mass and radius (and eventually the composition of their parent star) is known to be a degenerate problem. Proper analysis of observational data should therefore provide posterior distributions of internal structure parameters (e.g. core mass, mass fraction of gas) that take into account both the intrinsic degeneracy and the observational uncertainties in a fully bayesian approach. With Yann Alibert, Jonas Haldemann and colleague from Heidelberg, we are using a new type of neural network, conditional Invertible Neural Network, in order to compute the posterior distribution of internal structure parameters of planets observed in transit. A schematic overview of the principle of the cINN is shown below. During training the cINN learns to encode all information about the physical parameters x in the latent variables z (while enforcing that these follow a Gaussian distribution), that is not contained in the observations y. At prediction time, conditioned on the new observation y, the cINN then transforms the known prior distribution p(z) to x-space to retrieve posterior distribution p(x|y).
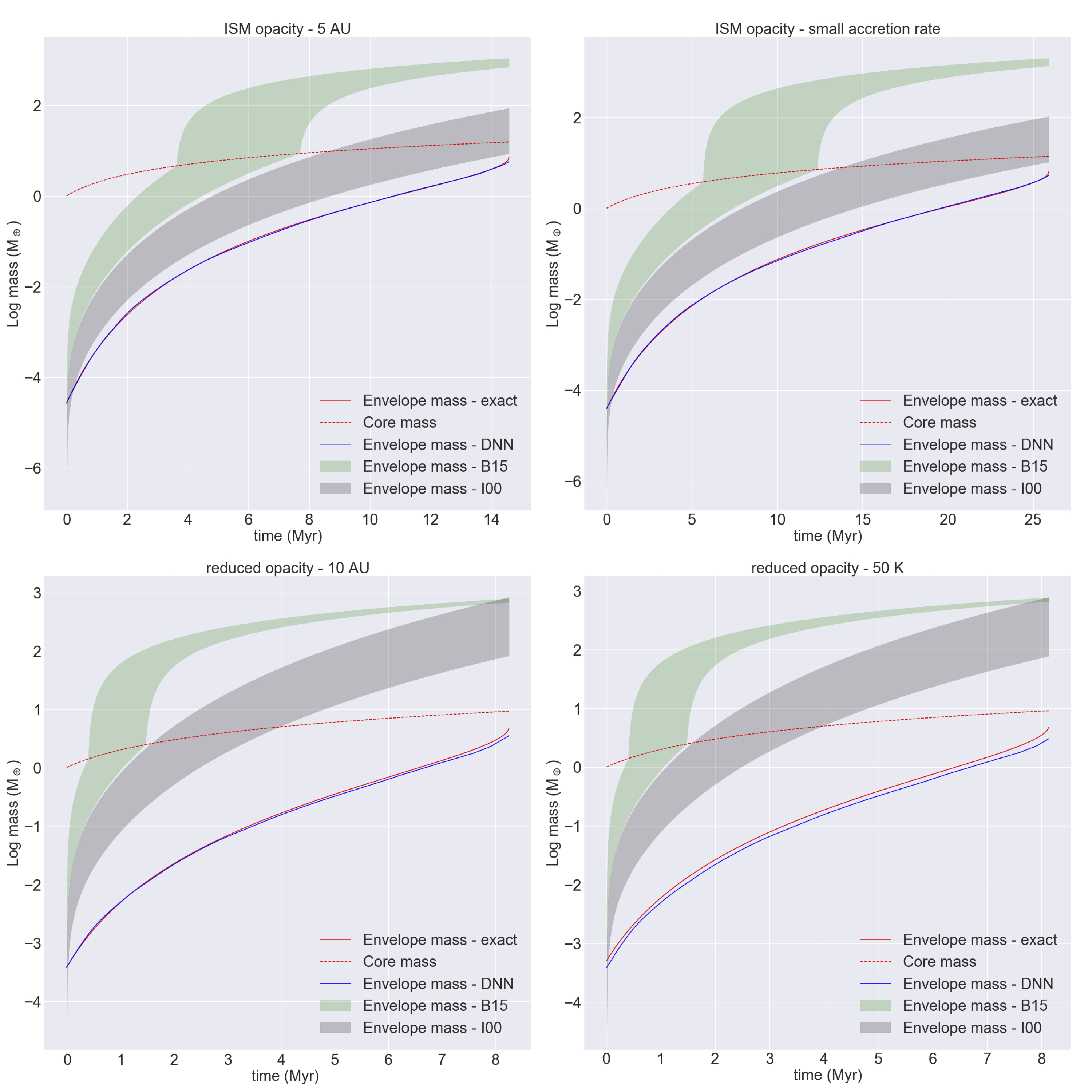
Predictions for PLATO
We use results of planet formation models coupled with the expected PLATO observational bias, as well as expected radial velocity performances, in order to predict the yield of PLATO. This project is developed with Thibaut Roger, and the figure below shows a preliminary result.