51 Pegasi b is the famous object Michel Mayor and Didier Queloz discovered in 1995 – an exoplanet around a star in the constellation Pegasus. The star was labelled 51 Pegasi by English astronomer John Flamsteed in 1712 in his star atlas. The lowercase letter “b” indicates that it was the first exoplanet discovered orbiting its host star. Other star catalogues used for naming exoplanets are for instance Wilhelm Gliese’s index (GJ) or HD named in honour of Henry Draper whose widow donated the money to finance it. Exoplanets can also be named after astronomical projects like the ground-based Hungarian Automated Telescope Network (HAT) or their discovering space observatory. Kepler-34(AB)b is an exoplanet that was found by NASA’s Kepler space telescope. It orbits the object Kepler-34 consisting of two Stars A and B. The exoplanet’s name shows that it circles around both of the stars in the binary system. Soon there will be nicer names for some selected exoplanets. The International Astronomical Union started a contest to give popular names to exoplanets along with their host stars.

http://www.iau.org/public/themes/naming_exoplanets/

The constellation of Pegasus in Flamsteed’s star map. Credit: BLR/www.RareMaps.com

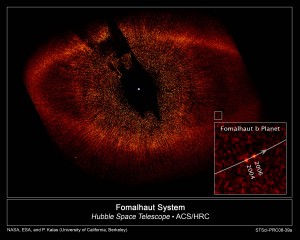
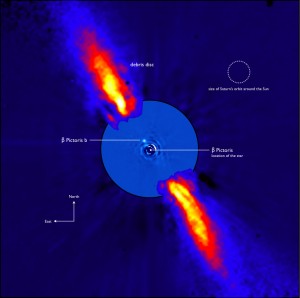
After the first exoplanet was discovered in 1995 by measuring the gravitational influence of the planet on its star by the radial velocity method, we had to wait 13 years to have the first true picture of an exoplanet. It was taken by the Hubble Space Telescope in 2008. The object is called Fomalhaut b, a planet that is 4 times the Sun-Neptune distance from its star. Its mass is estimated between 0.5 and 2 times that of Jupiter. Already in 2004 astronomers used ESO’s VLT to produce an image of a companion of a so called brown dwarf. To date, only about fifteen planets have been photographed.

The Fomalhaut system imaged by the Hubble Space Telescope. Credit: NASA/ESA/P.Kalas, UC Berkeley

1901 known exoplanets were listed in March 2015 by the Extrasolar Planets Encyclopaedia. The catalogue is regularly updated and steadily growing. There are over 3000 so called candidates that wait for confirmation. Planets seem to be very common objects in the universe – the rule rather than the exception. An average galaxy like our Milky Way contains about 100 billion stars. Analysing data of NASA’s Kepler space observatory astronomers have estimated that there are at least 100 billion planets just in our galaxy.

http://exoplanet.eu

http://www.caltech.edu/content/planets-abound

The Milky Way above the ESO 3.6-metre telescope with its exoplanet hunter HARPS in La Silla. Credit: ESO

It is practically impossible to directly observe a planet because its light is about a million times weaker than that of its star. It’s a bit like trying to see a firefly placed next to the lighthouse of a car. So that’s why we had to develop so-called indirect techniques like:

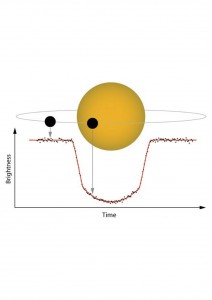
Transits, when looking at the drop in brightness of a star when a planet passes in front of it. The intensity of the drop is proportional to the size of the planet.

Transit technique. Credit ESO.

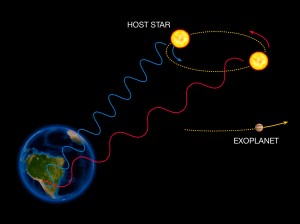
Radial velocities, when measuring the change in speed of a star caused by the presence of a planet. The value of the speed is proportional to the mass of the planet.

Radial Velocity technique. Credit ESO.

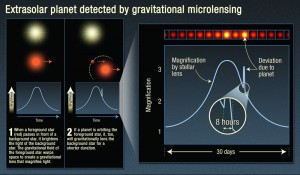
Gravitational Lens, when taking advantage of the passage of a planet in front of a very massive object which affects the light emitted by the planet.

Gravitational microlensing technique. Credit Nasa, Esa and A.Field (STScI)

Astrometry, by observing the movement of a star, we can deduce the mass of the planet if the star shows an eliptical movment.

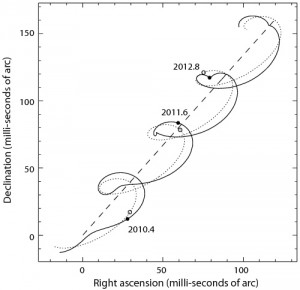
Path of a star viewed of a distance of 50pc and orbited by a 15Mj planet with a semi-major axis of 0.6 UA. Credit ESA.

But thanks to advances in technology we start now to be able to detect some planets directly. These techniques are very difficult to implement and need the use of a cotonograph wich hide the star. It’s why only a dozen has been photographed until today.

The Beta pictoris star is hidden by a coronograph, what allows to see its planet. Credit ESO.